あまり仕事では使わないのですが、趣味的に統計を勉強したくなったので、しばらく学習していました。範囲が広く、途中で挫けそうでしたが、なんとか合格することができました。
勉強中、「統計検定準1級合格の感想と出題範囲の個人的要点|うぇるち_憂いの篩」 の記事にとても励まされていたので、自分も学習メモを残しておきます(自分はこんなにしっかり勉強できてないと思いますが)。
最初に結果
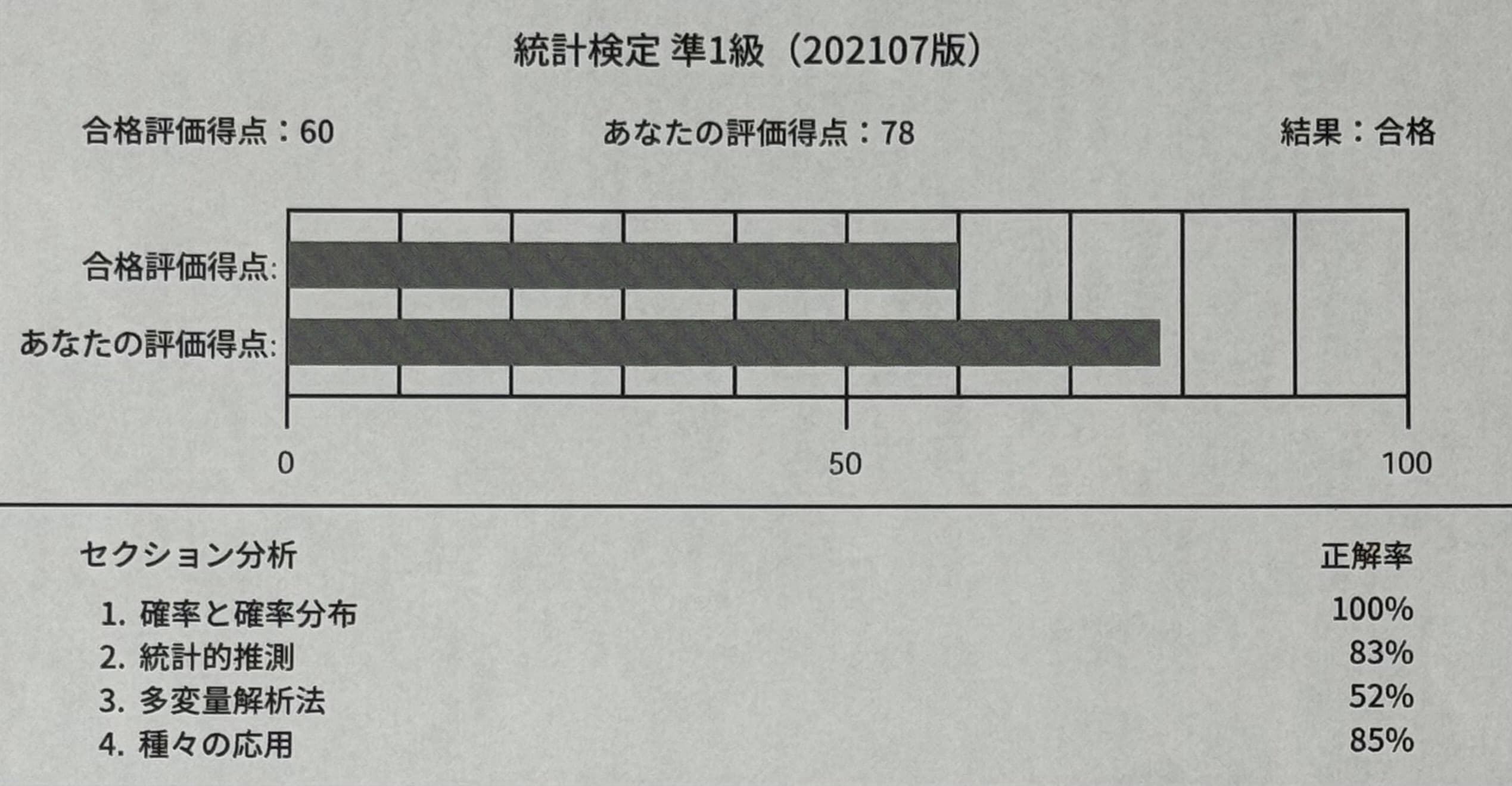
だいたい300時間ほど勉強して、78点で準1級に合格しました。5年前に2級は取っていて、そこから統計に触れていなかったのですが、久しぶりにしっかり勉強しました。

統計検定準1級とは
統計検定のHP では、以下のように書かれています。
大学において統計学の基礎的講義に引き続いて学ぶ応用的な統計学の諸手法の習得について検定します。具体的には下記の(1)、(2)を踏まえ、適切なデータ収集法を計画・立案し、問題に応じて適切な統計的手法を適用し、結果を正しく解釈する力を試験します。
(1)統計検定2級の内容をすべて含みます
(2)各種統計解析法の使い方および解析結果の正しい解釈
また、別のページ によると「大学の専門課程レベル」に相当するとのことです。
試験時間は90分、100点満点で60点以上が合格となります。
CBT方式の受験(ネット試験)が可能で、全国にある試験会場から日程を選んで受験できます。
勉強しようと思った理由
完全に趣味でやってみようと思いました。
一応きっかけとしては、生成AI関連の論文を読んだり、生成AIのキャッチアップをする中で、統計関連の知識が足りなくて理解が怪しい場面が何回かあり、一度しっかり理解しようと思ったというのがあります。
また、統計検定は統計学の知識を問う試験として優れているという印象があり、基礎をしっかり押さえるという意味で、良いマイルストーンになるなと考えました。(例えば こちらの記事 や こちらの記事 を読んでの印象です)
利用した参考書
メインで利用したのは「統計学実践ワークブック」です。準1級を受ける上で、ワークブックは必須かと思います。しかし、範囲がとても広く、ぱっと読むだけでは理解できない箇所も多くあり、進めていくのはなかなか大変でした。
ワークブックを読むだけでは理解できない場合に、補足用としてとけたろうさんの 統計検定®準1級講座【note+YouTube】 を購入して、勉強しました。
さらに問題演習用として、準1級の公式問題集を解きました。
最初に載っている2021年の過去問は 「極端に難しい」と言われている のを見て、解いていません。
学習の進め方
上記の通り、ワークブック中心に進めたのですが、普通に進めていくと終わらなそうだなと感じました。具体的に言うと、以下のように感じました。
試験範囲が広く、すべて理解しようとすると時間が膨大にかかる
解説を読んだだけでは理解できないところが多い
上記2点の理由で進みが遅くなると、1周目がなかなか終わらずしんどそう。また、1度学習してから次の復習までの時間が長くかり、定着の効率が悪そう
そこで、以下の方針で進めることにしました。
全てを理解することは諦め、重要そうな7〜8割程度をしっかり押さえる方針にする
「重要な知識」=「章末問題を解くために必要になる知識」と考えて進めました
最初から全てを学習するのではなく、重要なものから順に学習していく
1周目で最重要の50%程度を押さえ、2周目で次に重要なポイント、3周目でその次に重要なポイント(ここまでで80%程度)というようなイメージ
ワークブックの理解を促進するために補助の教材を使う
とけたろうさんの 統計検定®準1級講座【note+YouTube】 を購入して勉強しました
ChatGPT にもたくさん聞きました
結果的にまずワークブックを3周した後、解けなかった問題を解き直す形で4周目・5周目を進めました。その後で、公式問題集を解き、試験を受けました。
ワークブックの各章の内容と思ったこと
せっかくなので、各章で学習したことと、印象に残ったことを書いておきます。少し飛ばしてしまっているので、将来の自分のためにメモを残しておきます。
第1章: 事象と確率
ここの章はもともと知っている内容が多く、新しく学習した内容はあまり多くありません。
離散的な値をとる確率変数の場合の、期待値と分散の計算方法
連続的な値をとる確率変数の場合の、期待値と分散の計算方法
第2章: 確率分布と母関数
基本となる章なので、どれも計算方法をしっかり覚えました。
累積分布関数、生存関数、ハザード関数の定義
周辺確率密度関数、条件付き確率密度関数の定義
確率母関数、モーメント母関数の定義と使い方
第3章: 分布の特性値
ここも基本となるので、しっかり押さえておきました。
共分散、相関係数の計算方法
特性値の性質
変動係数の定義
加重平均、幾何平均、調和平均の意味
分散共分散行列、相関行列の定義
第4章: 変数変換
難しかった章の1つです。最初飛ばしてましたが、3周目にしっかりやりました。
変数変換した場合の確率密度関数の求め方
ヤコビアンの定義
(飛ばした)「データの変換」
ヤコビアンよくわかってなかったので、ヨビノリさんの動画 で勉強しました。
第5章: 離散型分布
基本となる分布はしっかりと押さえました。数も多く大変でしたが、Notionにまとめを作って、怪しいものは何度も見直しました。
ベルヌーイ分布、二項分布、超幾何分布、ポアソン分布、幾何分布、負の二項分布、多項分布の意味と確率関数
第6章: 連続型分布と標本分布
こちらも基本となる分布はしっかりと押さえました。離散型分布と同様にNotionにまとめを作りました。
正規分布、指数分布、t分布、F分布、カイ二乗分布の意味
ガンマ分布、ベータ分布の意味
(飛ばした)コーシー分布、対数正規分布、2変量正規分布、多変量正規分布、混合正規分布
ガンマ分布、ベータ分布は逃げられるかと思ったら全然逃げられなかったので、途中のタイミングでしっかり学習しました。けっこう飛ばしてしまいましたが、少なくとも2変量正規分布、多変量正規分布はやるべきだった気がします。
第7章: 極限定理、漸近理論
中心極限定理とデルタ法をしっかり押さえて、他の部分は飛ばしてしまいました。
中心極限定理、連続修正の定義
デルタ法の定義
(飛ばした)上記以外のところ
第8章: 統計的推定の基礎
自分としては最も難しかった章な気がします。覚えることが多く、それぞれも難しいです。ChatGPTに聞きながら理解を深めていきました。
最尤法の定義と計算
統計量、順序統計量の定義
不偏推定量、有効推定量、十分統計量の意味
クラーメル・ラオの不等式、フィッシャー情報量の定義
一致性、漸近有効性、漸近正規性の意味
ジャックナイフ推定量の計算方法
第9章: 区間推定
この章は新しく覚えることはあまり多くない気がします。しっかりと計算できるようにしておきました。
分散の区間推定の計算
分散の比の区間推定の計算
多項分布の信頼区間の計算
多項分布の差の信頼区間の計算
第10章: 検定の基礎と検定法の導出
この章も新しく覚えることは多くないかと思います。第一種の過誤、第二種の過誤のところは、図を書いて覚えました。
第一種の過誤、第二種の過誤、検出力の意味
サンプルサイズ設計の計算
第11章: 正規分布に関する検定
この章も新しく覚えることはあまり多くなかったですが、「2つの群をプールした標本分散」の計算方法はしっかり覚えました。
1標本の平均の検定方法(分散が既知の場合、未知の場合)
2標本の平均の検定方法(分散が既知の場合、未知の場合)
1標本の分散の検定方法、2標本の分散の検定方法
第12章: 一般の分布に関する検定法
この章でも検定について扱います。ポアソン分布に関する検定は、ポアソン分布の平均と分散を覚えていれば推測できるので、覚えませんでした。
母比率の検定方法
母比率の差の検定方法
適合度検定の使い方
(飛ばした)尤度比検定
第13章: ノンパラメトリック法
組合せの計算ができれば、比較的覚えることは少ないので、ありがたい章でした。
ウィルコクソンの順位和検定、並べ替え検定の使い方
符号付き順位検定、符号検定の使い方
(飛ばした)クラスカル・ウォリス検定、順位相関係数
第14章: マルコフ連鎖
一度理解すれば、問題は安定して解きやすいのかなと思いました。
マルコフ連鎖の定義、推移確率行列の表現方法
定常分布の求め方
マルコフ連鎖のパラメータ推定の計算方法
第15章: 確率過程の基礎
難しかった章の1つです。3周目で腰を据えて取り組みました。
独立定常増分の定義
ブラウン運動の定義、パラメータ推定の計算
ポアソン過程の定義、パラメータ推定の計算
複合ポアソン過程の意味
(飛ばした)計数過程
第16章: 重回帰分析
演習問題で使う知識に絞って勉強しました。重回帰分析の結果をもとに質問される問題と、正則化パラメータを推測する問題をしっかり解けるようにしておきました。
決定係数、自由度調整済み決定係数の意味
L1正則化とL2正則化の意味と、代表的な手法の特徴
(飛ばした)「重回帰分析」「重回帰分析の検定」のところはほぼ読んでないです
第17章: 回帰診断法
4つの回帰診断図をしっかり読めるようにしておきました。
「残差プロット」の意味と読み方
「正規Q-Qプロット」の意味と読み方
「標準化残差の絶対値の平方根プロット」の意味と読み方
「leverageとCookの距離」の意味と読み方
第18章: 質的回帰
定義をしっかり覚えておけばあとは計算するだけになるので、定義をちゃんと覚えました。
ロジスティック回帰モデルの定義
プロビットモデルの定義
ポアソン回帰モデルの定義
(飛ばした)一般化線形モデル
第19章: 回帰分析その他
最初飛ばし気味だったのですが、2周目と3周目でしっかり押さえました。
タイプⅠトービットモデルの意味と尤度関数の求め方
Cox比例ハザードモデルの定義
カプラン・マイヤー推定量の意味
(飛ばした)ニューラルネットワークモデル
第20章: 分散分析と実験計画法
分散分析表の作り方を覚えてしまえば、あとは比較的簡単に解ける気がします。覚えるのが苦手な自分としては、この章は楽しみながら勉強できました。
フィッシャーの三原則の意味
分散分析表の作成方法
直交表の意味と使い方
第21章: 標本調査法
比較的軽めの章かと思います。ネイマン配分法はしっかり押さえておきました。
様々な標本抽出法の意味
ネイマン配分法の計算方法
第22章: 主成分分析
章末問題が比較的簡単だったので、学習内容が薄めになってしまいました。大事な部分だと思うので、もう少し厚めに勉強するべきでした。また改めて勉強しようと思います。
主成分の寄与率、主成分得点の意味
主成分負荷量の定義
(飛ばした)平均偏差行列の特異値分解、自己符号化器
第23章: 判別分析
難しかったこともあり、全体的に飛ばし気味になってしまいました。ここもどこかでちゃんとやりたい...。
フィッシャーの線形判別関数の定義
サポートベクターマシンの特徴
(飛ばした)正準判別分析、混同行列とROC解析
(飛ばした)章末問題の23.3
第24章: クラスター分析
最近隣法、最遠隣法、K-means法に絞って、しっかり学習しました。
階層的手法のやり方(最近隣法、最遠隣法)
非階層的手法のやり方(K-means法)
(飛ばした)混合分布とEMアルゴリズムによる非階層的クラスタリング
第25章: 因子分析・グラフィカルモデル
この章も章末問題が比較的簡単だったので、学習内容が薄めになってしまいました。
因子分析の意味、因子負荷量の定義
バリマックス回転の意味
パス係数の求め方
(飛ばした)多因子モデルの因子分析、グラフィカルモデル
第26章: その他の多変量解析手法
この章はエッカート・ヤング分解をしっかり押さえて、他の理解は浅めになってしまいました。
エッカート・ヤング分解
(飛ばした)正準相関分析、数量化法・対応分析
第27章: 時系列解析
内容に対して、章末問題が比較的簡単な気がします。飛ばしてしまったところも多いです。ただ、自己回帰過程と移動平均過程はしっかり学習しました。
自己共分散、自己相関係数
定常性、ホワイトノイズ
自己回帰過程、移動平均過程
ダービン・ワトソン検定
(飛ばした)自己回帰移動平均過程、ラグ多項式、スペクトラム、ペリオドグラム、状態空間モデル
第28章: 分割表
章の前半はしっかりやりましたが、後半は飛ばしてしまいました。
分割表の意味
前向き研究と後向き研究の意味
母数の推定方法
(飛ばした)フィッシャーの正確検定、2×2分割表、2元分割表、3元分割表、グラフィカルモデル
(飛ばした)章末問題の28.3
第29章: 不完全データの統計処理
この章も章末問題のところだけにフォーカスして、内容を絞っての学習となりました。
欠測メカニズムのそれぞれの意味
削除法と補完法
(飛ばした)正規分布における推測、EMアルゴリズム
第30章: モデル選択
AICとBICをしっかり押さえました。章末問題の証明のところはサボってしまっています...。
AIC、BICの意味と選択方法
クロスバリデーション、過学習の意味
(飛ばした)章末問題の30.1
第31章: ベイズ法
内容が重くて、一部飛ばしてしまいましたが、すべて大事な内容かと思います。どこかでまた復習したいです。
ベータ二項モデル、ガンマ・ポアソンモデルの定義
MHアルゴリズムの手順と意味
(飛ばした)ギブス・サンプリング
(飛ばした)章末問題の31.2(2)、31.4
第32章: シミュレーション
章末問題の解き方をしっかり理解しただけで、全体的に理解は浅めでした。
モンテカルロ法
(飛ばした)乱数生成、モンテカルロ積分、ジャックナイフ法とブートストラップ法
終わりに
各章の内容を書くだけで、すごく時間がかかってしまいました。やっぱり範囲はとても広いなと思います。
特にワークブックの1周目をやっている時は全然終わりが見えず、絶望していましたが、粘り強く勉強を続けていくうちに徐々に理解が深まっていき、なんとか合格にたどりつけて本当に良かったです。
統計や機械学習は今後も細々と勉強を続けていけたらと思っているので、引き続き頑張りたいです。
Share this post


